Bayesian modelling and computation hand in hand in the age of massive datasets

Make the most out of the data at hand…

But how to effectively leverage the wealth of available data sources and extract as much value as possible for the problem tackled? This broad concern encompasses a series of questions that every statistician needs to consider prior to the actual analysis. Are the datasets collected of good quality? Are they relevant to the question asked? Is there reasonable chance for the signal of interest to be extracted? If these questions all have a positive answer, then what statistical approach can be used to best interrogate the data?

There is no unequivocal statistical recipe that addresses this last question, and this will sound particularly evident to those of you who have read the excellent blog post “Which models are useful?” by Dr Paul Kirk. Here, we will explore how useful answers may be obtained using Bayesian statistics, which is the specialty of many of us at the BSU. As you may know, Bayesian statistics are often put in opposition to frequentist statistics. But the goal of this article is not to provide a general introduction to the field, rather we will attempt to give a sense of its promises and pitfalls in the context of large biomedical studies.

Take the example of statistical genetics…

Typical tasks involve finding subgroups of patients based on their genetic profiles or finding gene signatures that are predictive of susceptibility to certain diseases. For example, a whole segment of COVID-19 research in which the BSU is involved aims at identifying the genetic contribution to the disease, as a step towards developing a therapeutic drug. But with millions of genetic variations, researchers are left with as many candidate biomarkers and an untold number of hypotheses for their modes of action within the complex molecular machinery controlling the immune system.

One way to go is to test for association between the disease and each and every genetic variant, one-by-one, using a simple univariate model.

Figure 1: Univariate testing. Each square represents a single test, carried out separately from the other tests.

While this may successfully unmask promising biomarkers¹, there is hope for more powerful inference to be obtained using a model that would represent how genetic variants act in concert to modulate the clinical expression of the disease. In particular, it is important to develop statistical approaches for and with respect to the intrinsic characteristics of the biological data considered.

Bayesian hierarchical modelling for flexible information-sharing…

Bayesian modelling provides us with a flexible framework towards this, as it permits leveraging complicated dependences within and across heterogeneous sources of information (such as clinical parameters, genetic variants as well as other molecular entities and annotations on these entities). In particular, it allows us to construct joint models in a hierarchical fashion, thereby enabling information to be “borrowed” across different problem features and samples. It also permits incorporating contextual prior information where desirable, while coherently conveying uncertainty.

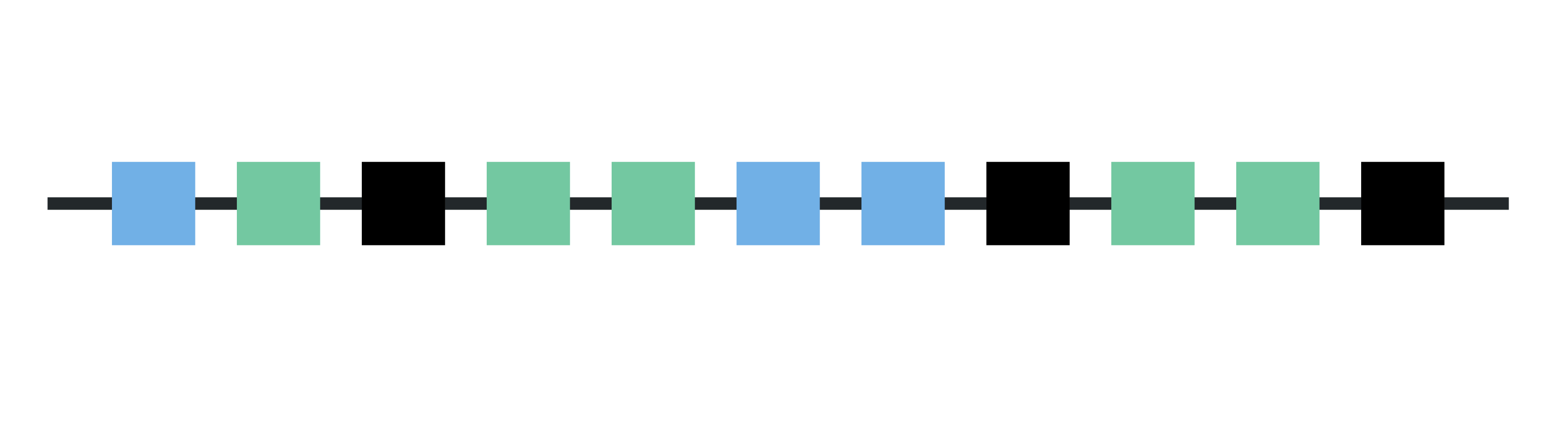Figure 2: Bayesian hierarchical modelling, jointly accounting for prior information and dependence patterns.

It turns out that this holistic modelling perspective, tailored to the problem and data at hand, is very much in line with the so-called systems biology view, dating back to the advent of high-throughput technologies:

Bridging the gap…

But this is not the end of the story. Indeed, this ambition of studying biological systems as a whole often faces practical difficulties when it comes to accommodating all candidate actors within a single model: that of the computational feasibility of estimating jointly the very large number of parameters for representing these actors.

Figure 3: Bayesian inference for very large parameter spaces. In genetic applications but not only, model parameters can number in the millions, which presents a computational challenge for joint inference, both in terms of runtime and memory usage.

This concern has long been particularly acute, and even prohibitive, in the context of Bayesian inference. And still today, classical Markov Chain Monte Carlo (MCMC) algorithms — the workhorse of Bayesian inference since the 1990s — are frequently labelled impractical for exploring spaces exceeding a few dozens of parameters, that is, orders of magnitude smaller than the numbers encountered in today’s applications. (Note that problems can be large in terms of number of samples or variables, and these scenarios correspond to very different statistical paradigms, but we won’t discuss this here.)

The development of novel MCMC algorithms and that of scalable approximate inference algorithms (such as expectation propagation or variational approaches) concomitant with the advances in Machine Learning, has alleviated this issue, but the tension between flexible joint modelling and scalability of inference for these models remains important. These modelling and algorithmic aspects therefore need to be thought of hand in hand: models should lend themselves to efficient inference and inference algorithms should in principle be model specific. Moreover, tractability should not come at the expense of accurate inference for the specific data and statistical task of interest.

An interdisciplinary collaborative effort…

Clearly, all this can only be achieved as part of a close collaborative effort with biologists, clinicians, computer scientists and epidemiologists. This interdisciplinarity creates a virtuous self-feeding circle, which opens new avenues for understanding biology, but also pushes forward innovation in other basic and applied science disciplines, towards tangible benefits for our societies. Quite exciting.

References

L. Strausberg. Talkin’ Omics. Disease Markers, 17:39, 2001. Welter, J. MacArthur, J. Morales, T. Burdett, P. Hall, H. Junkins, A. Klemm, P. Flicek, T. Manolio, and L. Hindorff. The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Research, 42:D1001–D1006, 2014.